跳表的实现

(Updated: )
数据库
, ,

跳表的实现

在计算机科学中，跳跃列表是一种数据结构。它使得包含 n 个元素的有序序列的查找和插入操作的平均时间复杂度都是$O(\log n)$，优于数组的 $O(n)$ 复杂度。

什么是跳表

跳表是对有序链表的改进, 在有序链表的基础上增加了 分层 的概念。首先，跳表的每一层都是一个有序链表，特别地，最底层是初始的有序链表。每个位于第 i 层的节点有 p 的概率出现在第 i+1 层，p 为常数(通常为 $\frac{1}{2}$ 或 $\frac{1}{4}$)。

跳表

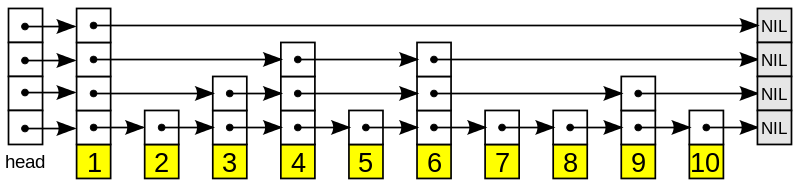
  • 跳表是是分层的链表

  • 跳表的每一层都是有序链表

  • 跳表的最底层是完整的有序链表

跳表的结构看起来像个树, 查询、插入和删除的复杂度也是 $O(\log{n})$ (最坏复杂度是 $O(n)$, 每层有哪些节点是通过概率得到的，因此最坏可能每一层都是一个完整的链表)。

具体实现

节点的设计

一个节点要存储这个节点所在的每一层的下个节点的指针，使用一个数组来存储 forward(Node **)。

1
2
3
4
5
6
7
8
9
10
struct Node {
  K key;
  V value;
  Node **forward; // Node*[] 存储每层的下一个节点
  int level;
  Node(K key, V value, int level) : key(key), value(value), level(level) {
    forward = new Node *[level + 1];
  }
  ~Node() { delete[] forward; }
};

获取节点的最大层数

每个位于第 i 层的节点有 p 的概率出现在第 i+1 层

模拟这个过程即可

这里使用到了 rand() 这个随机函数, 为了保证随机性，同时也要使用设置 srand(time(0)) 来保证随机性, 更推荐用 C++11 的随机数生成设施替换 rand() 。

1
2
3
4
5
6
7
8
9
10
11
constexpr int MAX_LV = 32;
constexpr int P = 4;
constexpr int S = 0xFFFF;
constexpr int PS = S / P;

auto random_level() -> int {
  int lv = 0;
  while ((rand() & S) < PS)
    ++lv;
  return MAX_LV > lv ? lv : MAX_LV;
}

查找

在跳表中查找，就是从第 $L(n)$ 层开始，水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层。重复这个过程直至到达第一层且无法继续进行操作。此时，若下一个节点是目标节点，则成功查找；反之，则元素不存在。这样一来，查找的过程中会跳过一些没有必要的比较，所以相比于有序链表的查询，跳表的查询更快。

跳表结构

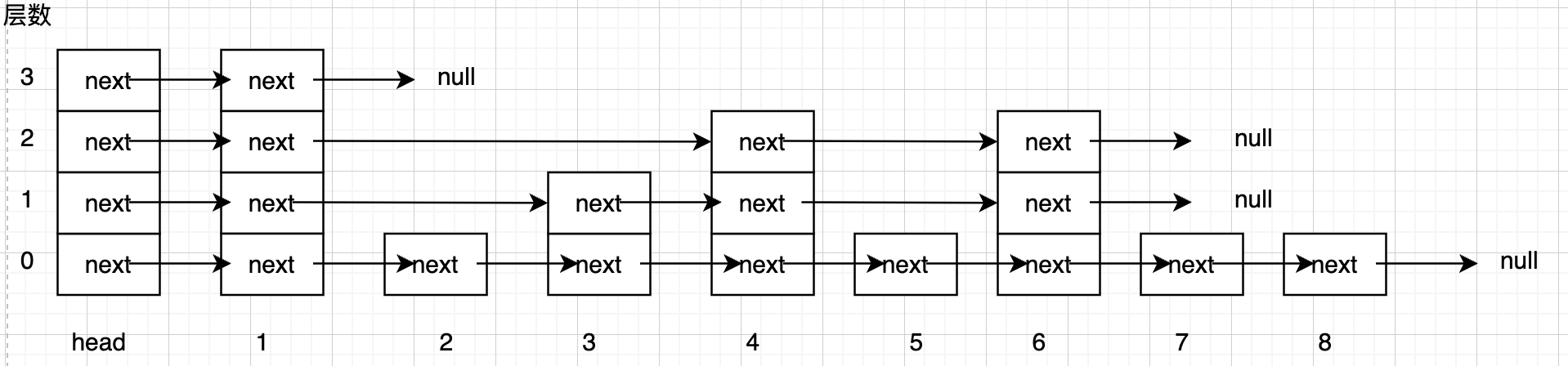
在这个 1-8 的跳表中查找 5 (这里演示的比较是严格小于)

查找 5

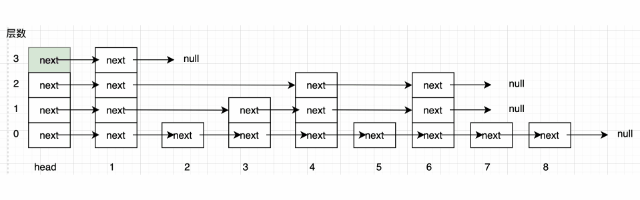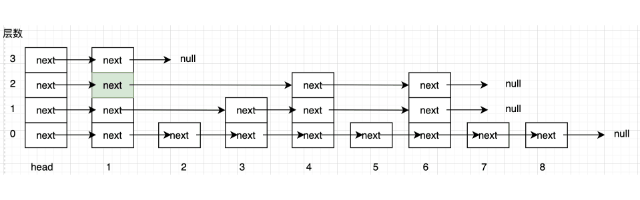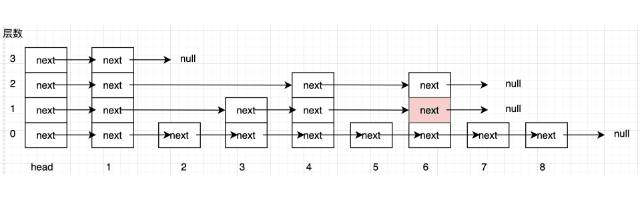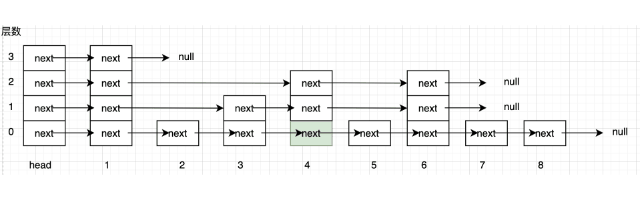
  • 开始是在第 3 层的 head 处，与他指向的下一个节点的值做比较 ($1 < 5$), 现在移动到了第 3 层的 1 节点处
  • 1 节点第 3 层的下一个节点不存在，现在移动到 1 节点的第 2 层
  • 与 1 节点第 2 层的下一个节点的值做比较 ($4 < 5$), 移动到 4 节点的第 2 层
  • 与 4 节点第 2 层的下一个节点的值做比较 ($6 > 5$), 移动到 4 节点的第 1 层
  • 与 4 节点第 1 层的下一个节点的值做比较 ($6 > 5$), 移动到 4 节点的第 0 层
  • 与 4 节点第 0 层的下一个节点的值做比较 ($5 = 5$), 下一个节点就是我们要找的值，这里使用了严格小于的比较方式，最后获得的是正确结果的前一个节点。

答案就是查找到的下一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
auto find(K key) -> V {
  if (size == 0)
    return 0;
  Node *tmp = head;
  for (int i = level; i >= 0; --i) {
    while (tmp->forward[i] != nullptr && cmp(tmp->forward[i]->key, key))
      tmp = tmp->forward[i];
  }
  if (tmp->forward[0] != nullptr && tmp->forward[0]->key == key)
    return tmp->value;
  return V{};
}

插入

插入与查找的过程类似，不同的是需要记录每一层要插入哪个节点的后面(使用 update 记录)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Node **update{new Node *[MAX_LV + 1]};

auto insert(K key, V value) -> void {
  Node *tmp = head;
  // 查找并记录每一层要插入到哪个节点的后面
  for (int i = level; i >= 0; --i) {
    while (tmp->forward[i] != nullptr && cmp(tmp->forward[i]->key, key)) {
      tmp = tmp->forward[i];
    }
    update[i] = tmp;
  }
  // 如果这个 key 已经存在了， 修改它的值
  if (tmp->forward[0] != nullptr && tmp->forward[0]->key == key) {
    tmp->forward[0]->value = value;
    return;
  }
  // 这个节点的最大层数，这个节点会在 [0, lv] 层存在
  auto lv = [&]() {
    int t = random_level();
    if (level < t) {
      t = ++level;
      update[level] = head;
    }
    return t;
  }();
  // 将新节点一次加入到 [0, lv] 中每层的有序链表中
  Node *new_node = new Node(key, value, lv);
  for (int i = lv; i >= 0; --i) {
    new_node->forward[i] = update[i]->forward[i];
    update[i]->forward[i] = new_node;
  }
  ++size;
}

删除

删除操作与插入操作相同，同样要记录这个节点在每一层的前一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
auto erase(K key) -> void {
  Node *tmp = head;
  // 查找并记录这个节点在每一层的前一个节点
  for (int i = level; i >= 0; --i) {
    while (tmp->forward[i] != nullptr && cmp(tmp->forward[i]->key, key))
      tmp = tmp->forward[i];
    update[i] = tmp;
  }
  // 这个节点不存在的话
  if (tmp->forward[0] == nullptr || tmp->forward[0]->key != key) {
    return;
  }

  // 从最底层向上层依次删除这个节点。
  auto p = update[0]->forward[0];

  for (int i = 0; i <= level; ++i) {
    if (update[i]->forward[i] != p) {
      break;
    }
    update[i]->forward[i] = p->forward[i];
  }
  delete p;
  // 删除节点可能会使层数降低 (例如：最上面一层只有 head 节点和要被删除的节点，删除节点后只剩 head 节点了，此时这一层也可以被删除)
  while (level > 0 && head->forward[level] == nullptr)
    --level;
  --size;
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
constexpr int MAX_LV = 32;
constexpr int P = 4;
constexpr int S = 0xFFFF;
constexpr int PS = S / P;

template <typename K, typename V, typename CMP = std::less<K>> struct SkipList {

  struct Node {
    K key;
    V value;
    Node **forward;
    int level;
    Node(K key, V value, int level) : key(key), value(value), level(level) {
      forward = new Node *[level + 1];
    }
    ~Node() { delete[] forward; }
  };

private:
  Node *head{new Node(K{}, V{}, MAX_LV)};
  Node **update{new Node *[MAX_LV + 1]};
  CMP cmp;
  int size{0};
  int level{0};

public:
  SkipList() { srand(time(0)); }

  ~SkipList() {
    delete[] update;
    for (Node *tmp = head; tmp != nullptr;) {
      head = head->forward[0];
      delete tmp;
      tmp = head;
    }
  }

  auto random_level() -> int {
    int lv = 0;
    while ((rand() & S) < PS)
      ++lv;
    return MAX_LV > lv ? lv : MAX_LV;
  }

  auto find(K key) -> V {
    if (size == 0)
      return 0;
    Node *tmp = head;
    for (int i = level; i >= 0; --i) {
      while (tmp->forward[i] != nullptr && cmp(tmp->forward[i]->key, key))
        tmp = tmp->forward[i];
    }
    if (tmp->forward[0] != nullptr && tmp->forward[0]->key == key)
      return tmp->value;
    return V{};
  }

  auto insert(K key, V value) -> void {
    Node *tmp = head;
    for (int i = level; i >= 0; --i) {
      while (tmp->forward[i] != nullptr && cmp(tmp->forward[i]->key, key)) {
        tmp = tmp->forward[i];
      }
      update[i] = tmp;
    }
    if (tmp->forward[0] != nullptr && tmp->forward[0]->key == key) {
      tmp->forward[0]->value = value;
      return;
    }

    auto lv = [&]() {
      int t = random_level();
      if (level < t) {
        t = ++level;
        update[level] = head;
      }
      return t;
    }();

    Node *new_node = new Node(key, value, lv);
    for (int i = lv; i >= 0; --i) {
      new_node->forward[i] = update[i]->forward[i];
      update[i]->forward[i] = new_node;
    }
    ++size;
  }

  auto erase(K key) -> void {
    Node *tmp = head;
    for (int i = level; i >= 0; --i) {
      while (tmp->forward[i] != nullptr && cmp(tmp->forward[i]->key, key))
        tmp = tmp->forward[i];
      update[i] = tmp;
    }
    // key is not exist;
    if (tmp->forward[0] == nullptr || tmp->forward[0]->key != key) {
      return;
    }

    auto p = update[0]->forward[0];

    for (int i = 0; i <= level; ++i) {
      if (update[i]->forward[i] != p) {
        break;
      }
      update[i]->forward[i] = p->forward[i];
    }
    delete p;
    while (level > 0 && head->forward[level] == nullptr)
      --level;
    --size;
  }
};

其他

OI-WIKI 跳表

维基百科 跳跃列表