CMU15-445 Lab2 : 可高并发的 B+ 树索引
B+ 树
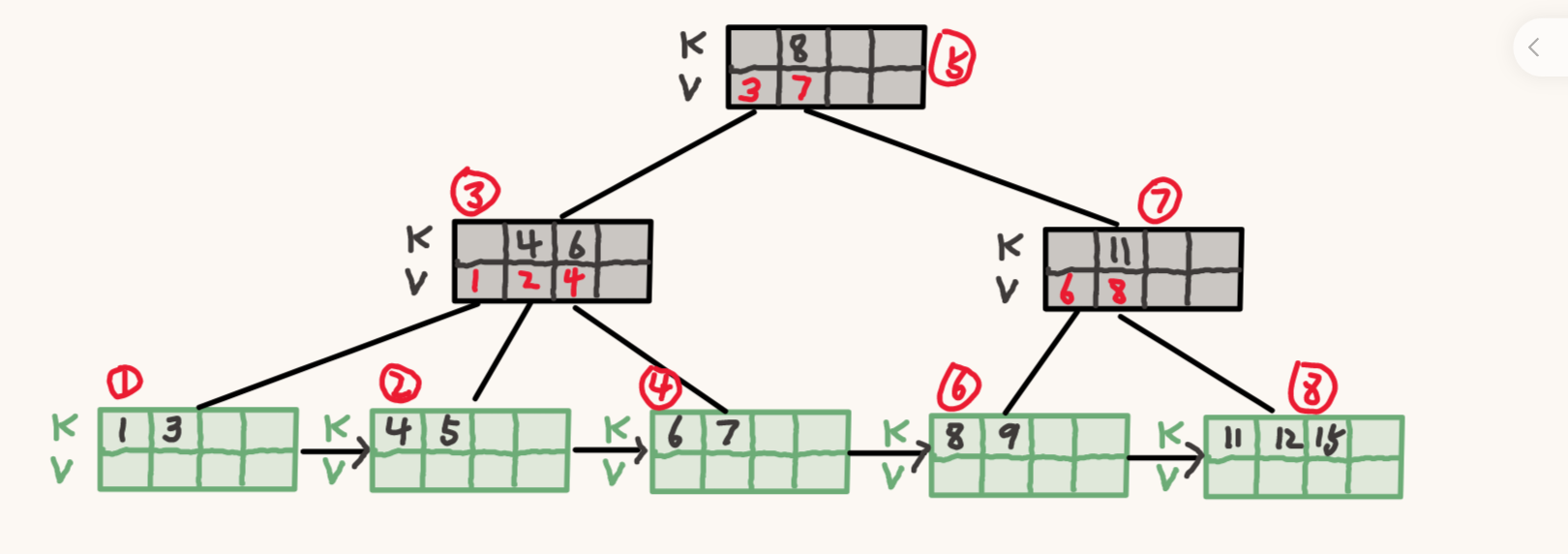
上图表示的是一颗四阶 B+ 树,四阶表示每个节点最多存四个 K-V 对。
B+ 树的叶子节点分为三类:
- 根节点
- 内部节点
- 叶子节点
根节点可以是内部节点也可使叶子节点。
B+ 树的每个节点不仅有最大容量,也有最小容量(最小容量 = 最大容量的一半, 下取整),低于最小容量的节点会想方法让自己的节点树增加(在 删除 中详细讲解),根节点没有最小容量限制。
每个节点中的数据是有序的,按照 K 值排序。
内部节点是不存储真实数据的,而是存储子树的位置。上图中的 3 号内部节点,他已经存储了 3 个 K-V 对,第一个 K-V 对指向 $K < 4$ 的子树的位置,第二个 K-V 指向 $4 \leq K < 6$ 的子树位置,第三个 K-V 对指向 $ 6 \leq K$ 的子树位置。
内部节点的 K 实际是一个范围。
叶子节点存储了真实的数据(也可以是指向数据的地址)。同时,叶子节点也会指向下一个叶子节点,像链表一样。
搜索
因为信息存放在叶子节点中,只要找到 key 所在的叶子节点, 递归查找即可。节点中的 key 是有序的,查找下一个节点可以借助二分查找。
插入
B+ 树的插入是自下而上的。
- 根据
key找到它该插入的叶子节点。 - 插入数据到这个叶子节点,判断这个叶子节点是否等于最大容量,若果是的话要进行分裂操作,否则什么也不做(也可以先判断再插入)。
- 分裂操作,将这个节点中的一半分到一个新节点,创建了新节点也要向父节点去插入一对 K-V 来确保父节点表示的范围正确, 这对 K-V 是新节点的第一对 K-V, 如果插入后的父节点等于最大容量,同样要进行分裂操作。(如果要分裂的是叶子节点,还需要更新下一个节点)。
现在考虑在一个 5 阶的 B+ 树上插入一个 (5, V) 。
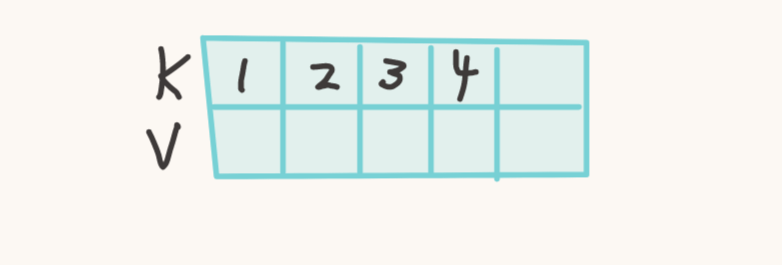
插入后这个节点的大小就等于最大容量了,要进行分裂操作。
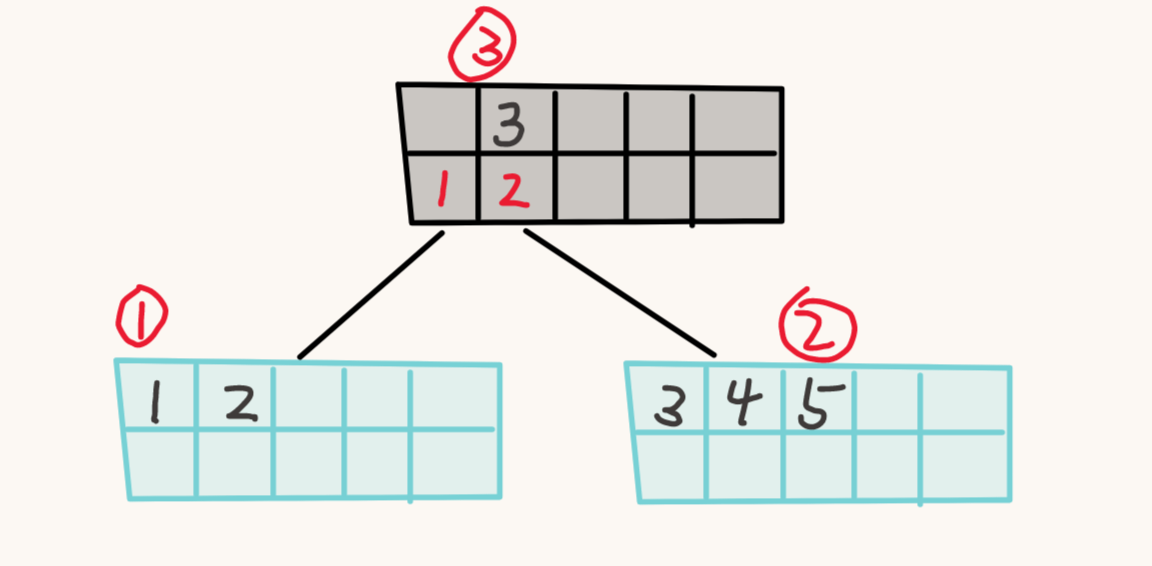
分裂之后,我们需要向它的父节点插入一个 K-V。
自下而上的插入,当还没有分裂时,根节点是一个叶子节点,同时大小为 1 的节点是不表示的,再没有插入 (5, V) 时,节点 3 是不表示的。
删除
删除操作也是自下而上的。
- 删除一个 K-V 后,如果这个节点的大小严格小于最小容量,需要进行合并操作。
- 优先考虑从同一个父亲节点的兄弟节点中拿走一个 K-V,被拿走的节点大小必须是严格大于节点的最小容量的。
- 如果不能进行拿走节点的操作,就要考虑把自己的所有 K-V 插入到周围的节点中,这个节点也就被删除了,对于它的父节点也要删除对应的 K-V, 接着考虑父节点是否需要进行合并操作

删除 key 值为 2 的 K-V。
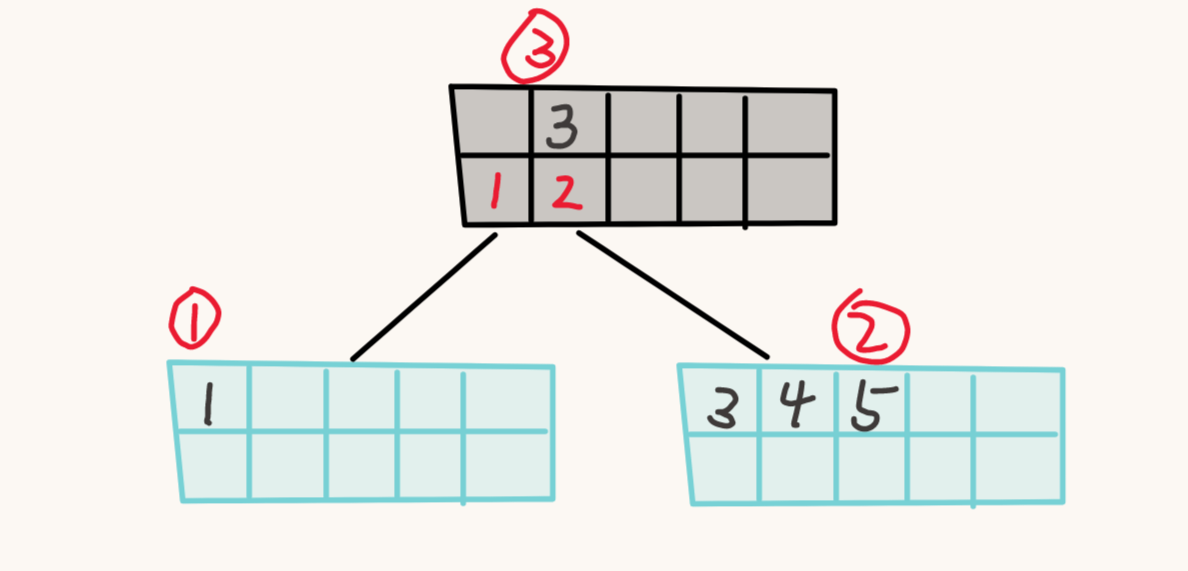
这时节点 1 的大小严格小于最小容量,尝试从节点 2 中拿一个节点,刚好 2 号节点的大小是严格大于最小容量的。
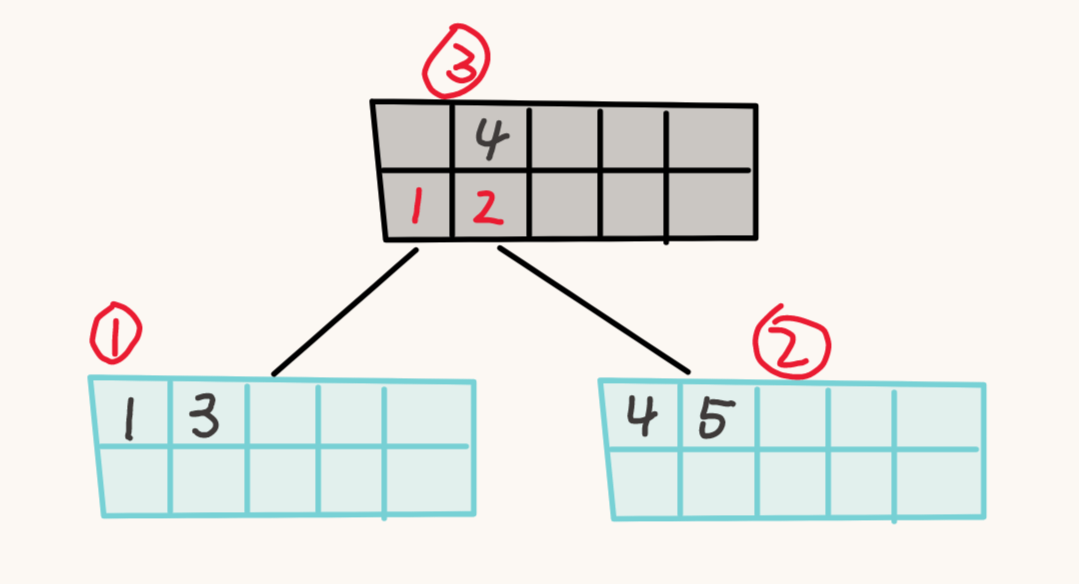
只能拿走 2 号节点的第一个 K-V,因此还需要对父节点中对应的 K-V 进行修改。
考虑删除 key 值为 3 的 K-V。
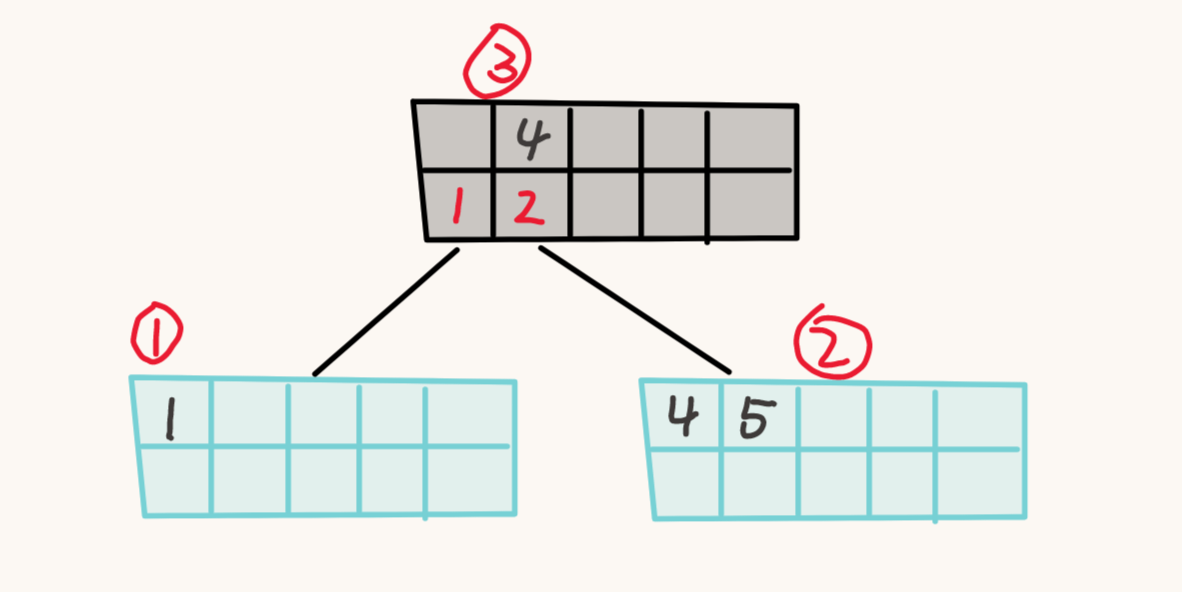
节点 1 的又需要进行合并操作,这时的 2 号节点不能提供一个 K-V 给 1 号节点了, 尝试将 2 号节点的 K-V 都移动到 1 号节点 (或者 1 移动到 2)。
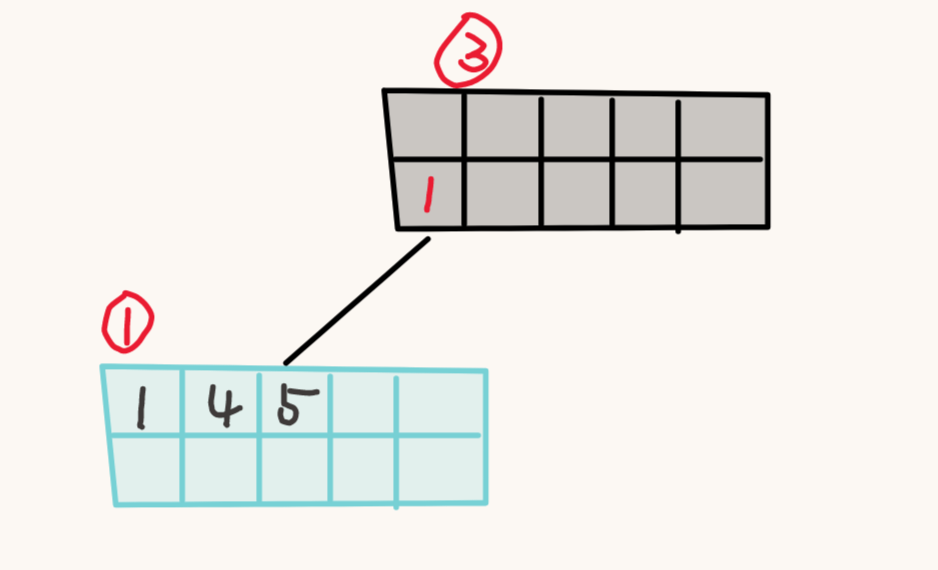
2 号节点不存在了,要删除父节点中对应的 K-V。
父节点 3 只剩一对 K-V 了,如果它可以进行合并操作,就要对他进行这个操作,这里不能进行操作。父节点 3 也没有存在的意义,删除节点 3 只保留节点 1 。
并发
最简单的想法是让 插入、删除、搜索 这三个节点共用一把读写锁,这样效率实在太低了。
采用特殊的加锁方式 “latch crabbing”, 像螃蟹走路一样进行加锁。先锁住父节点,在锁住孩子节点,如果孩子节点,如果孩子节点是安全的,就解开父节点的锁。
搜索
孩子节点一定是安全的,搜索不会改变任何节点的大小。
搜索 key 值为 12 的 K-V
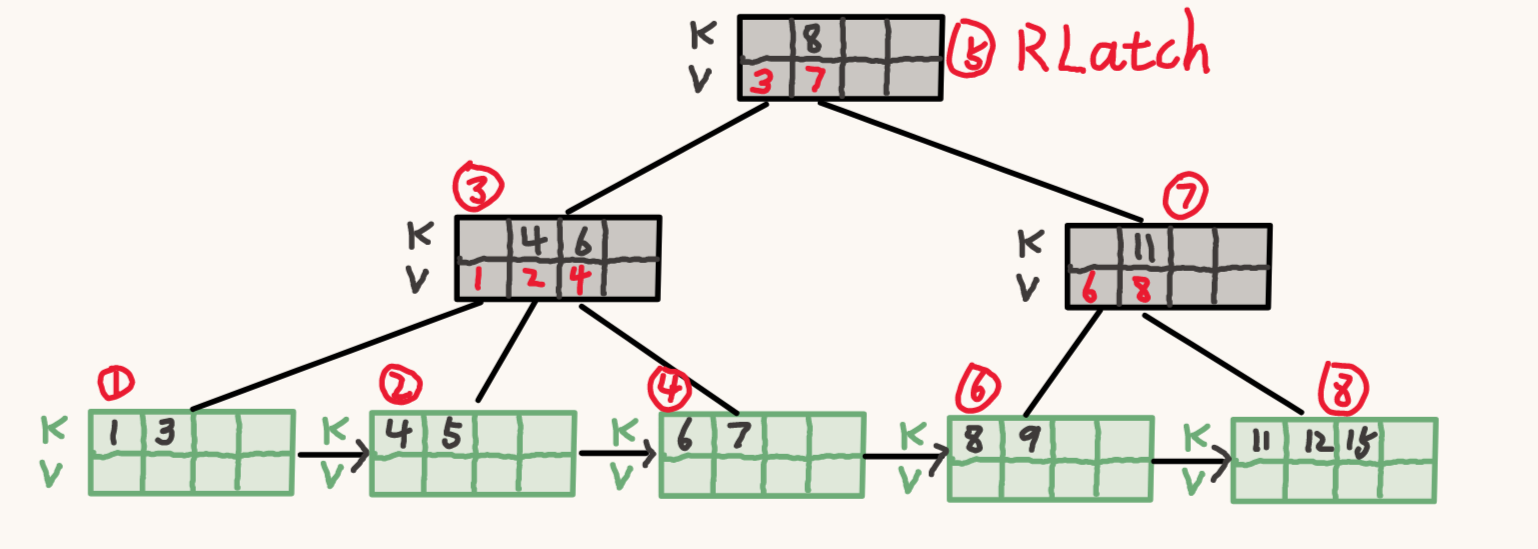
锁住孩子节点。/images/数据库/CMU15-445/B+树与高并发/2search2.png)
释放父节点。
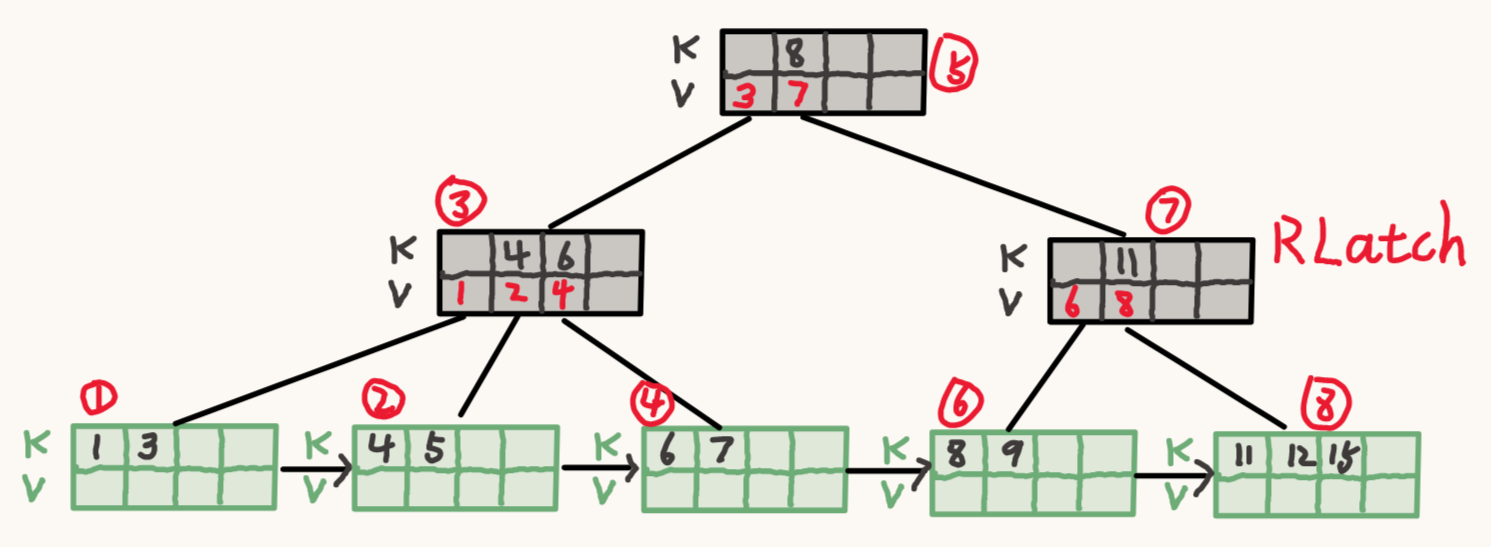
递归进行即可。
插入
插入操作会改变节点的大小,当前节点大小 + 1 等于节点的最大容量,这个节点就是不安全的,如果对这个节点进行插入操作,它的父节点也要进行插入操作,因此不能释放它的父节点的写锁。
如果在下面遇到了一个安全的节点,之前所有的上锁的节点都可以解锁了,包括之前不安全的节点,因为这个安全的节点保证了上面的节点不会被下面的操作影响。
插入 (2, V), 先锁住根节点。
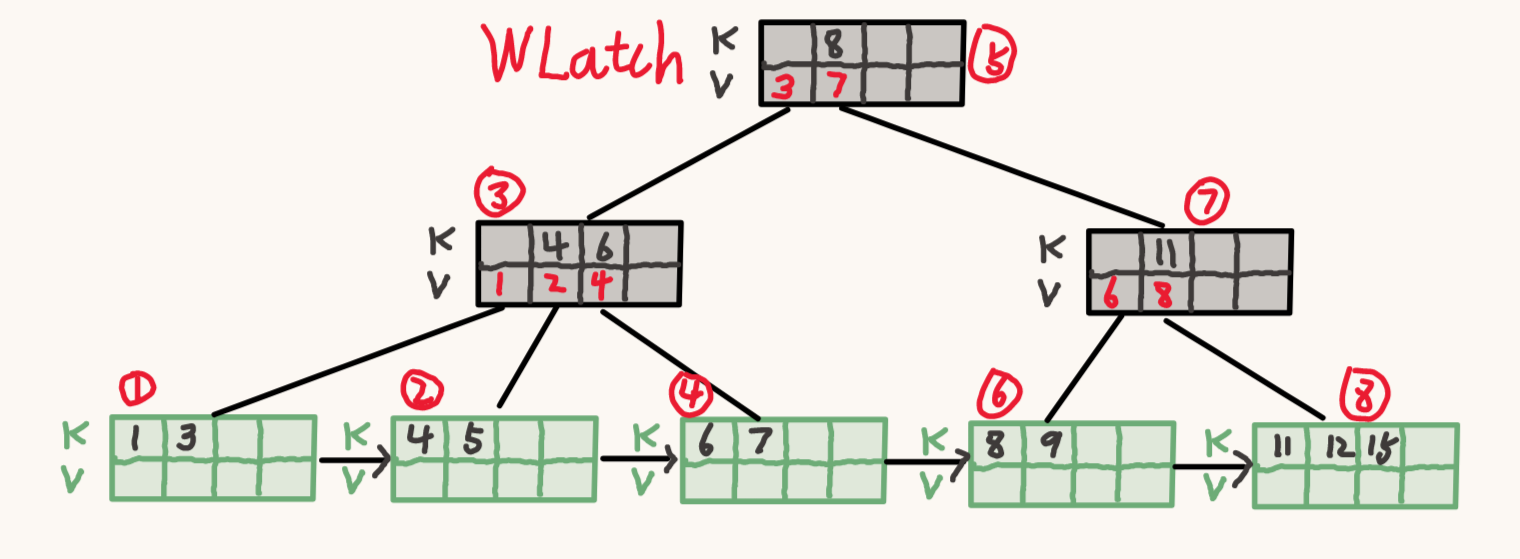
再锁住子节点 3,并判断他是否安全。
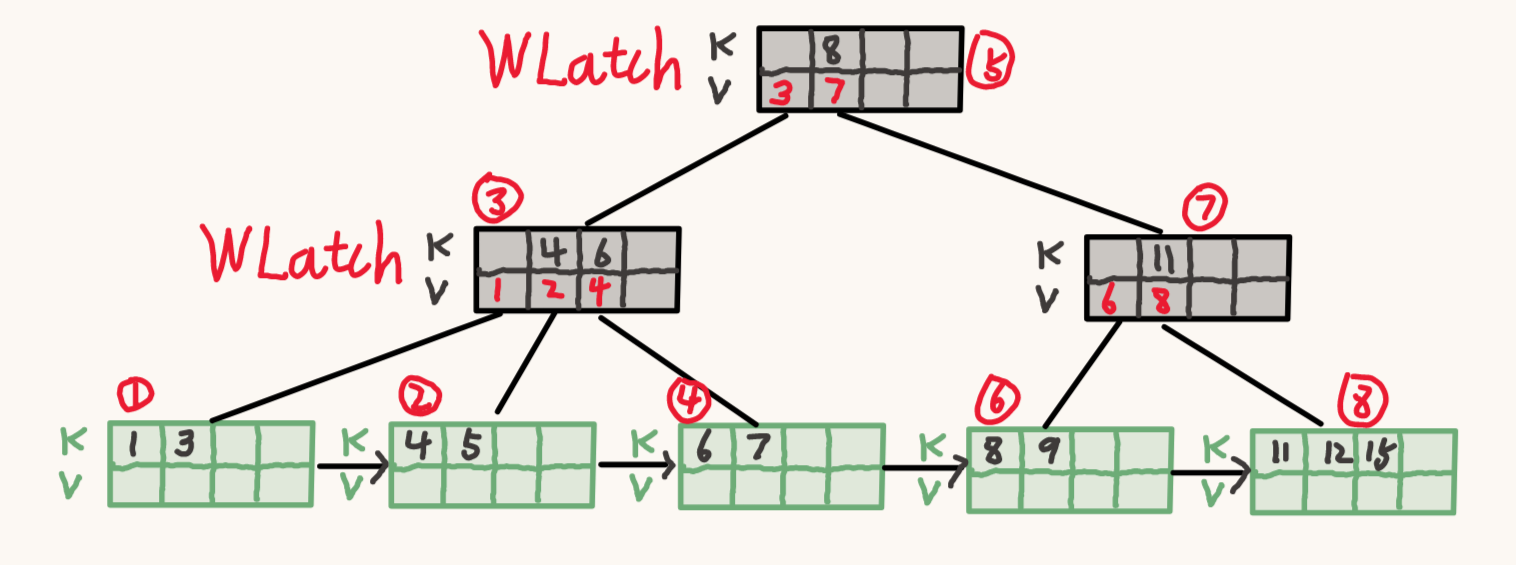
子节点 3 并不安全,不释放节点 5 的锁,继续递归对节点 1 加锁。
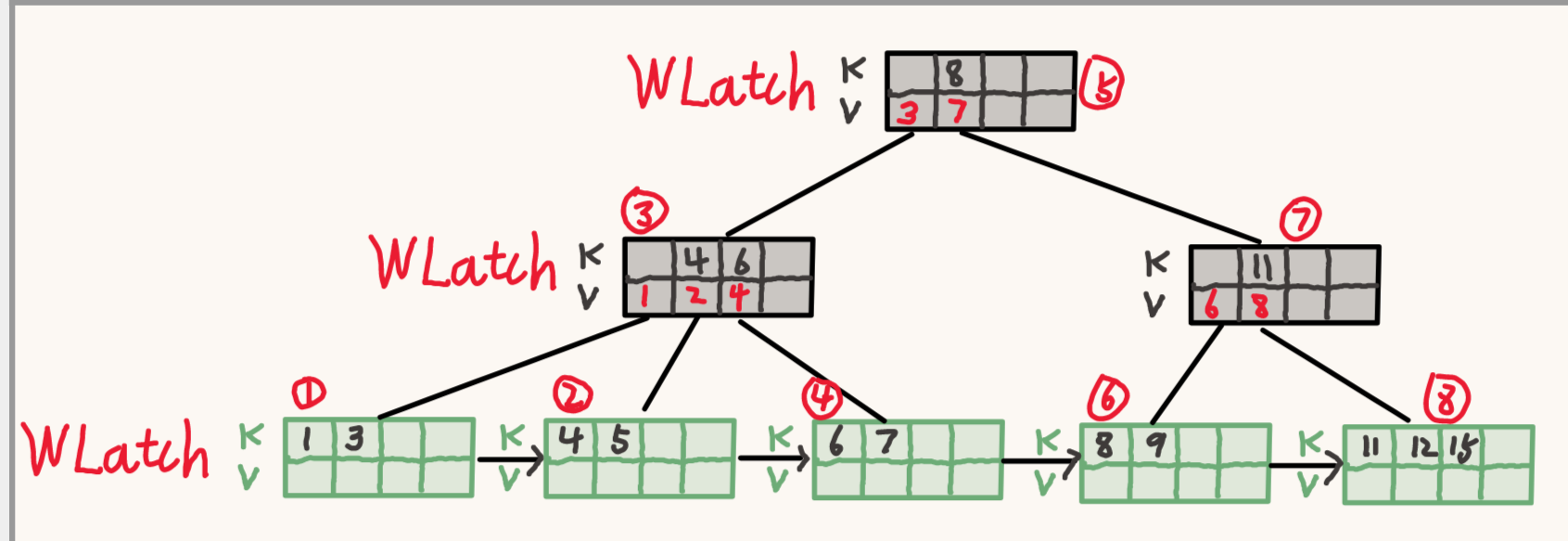
节点 1 是安全的,释放节点3,5 的锁。
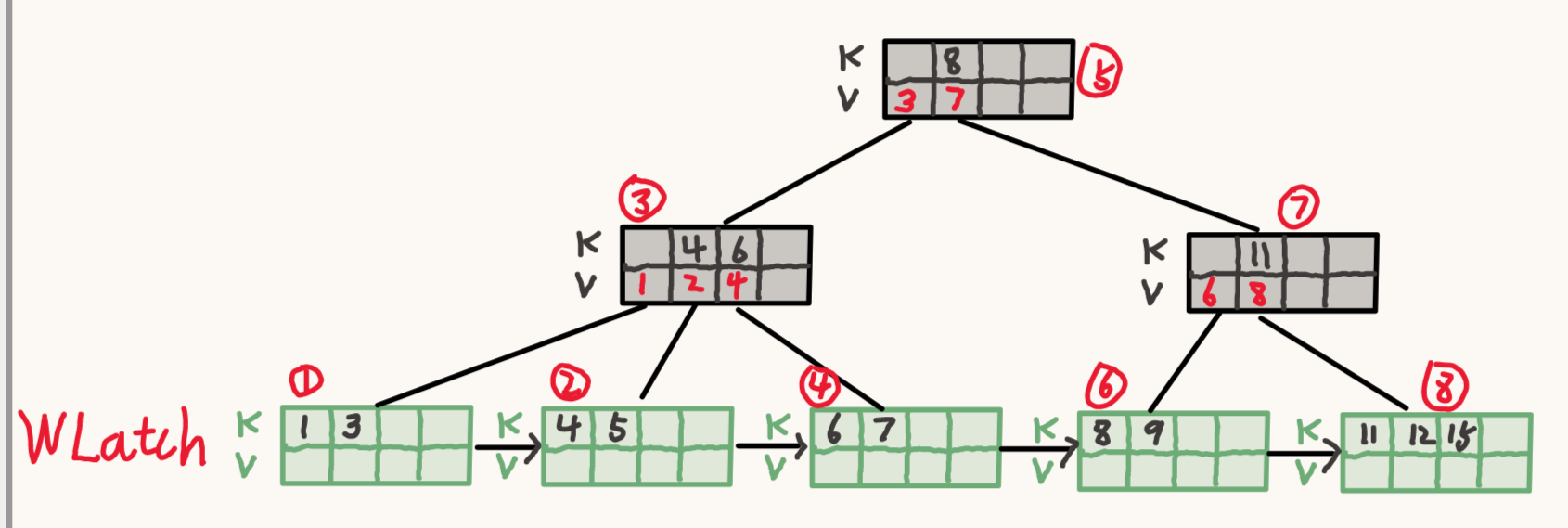
删除
与插入操作类似,虽然它有可能会更改多个节点,但是锁住父节点就没什么影响了。
判断节点是否安全的条件为,节点大小严格大于最小容量的节点是安全的,否则是不安全的。
Bustub 中的 Latch
Lock 与 Latch
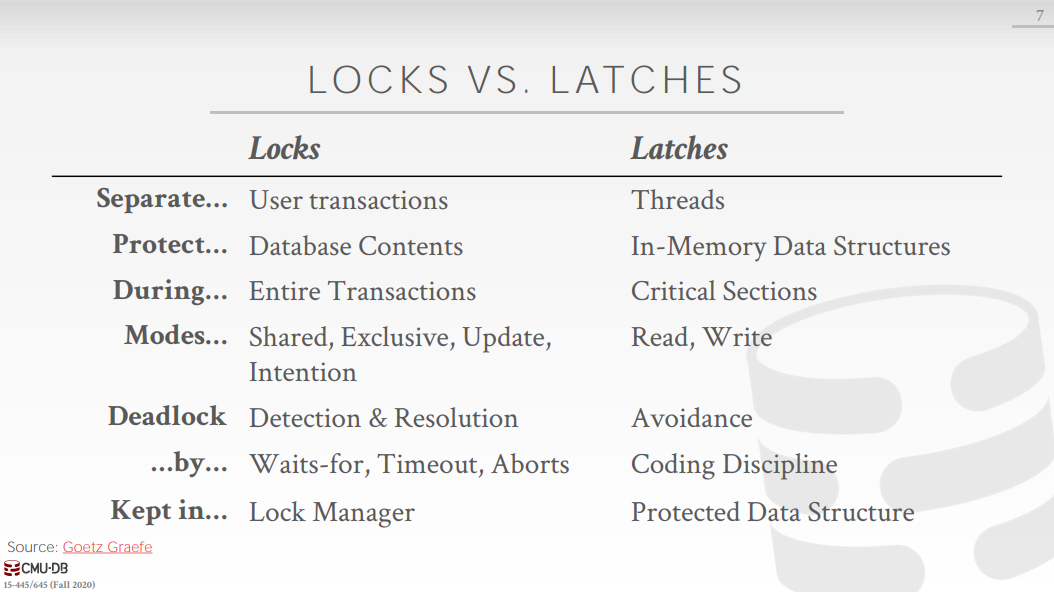
乐观的实现
insert 与 delete 时, 都会锁住先锁住根节点,这时其他线程不能读也不能写, 根节点的写锁成为了并发的瓶颈。
很多操作是不需要 split 与 merge 操作的, 也就是说在这些操作中叶子节点不会对父节点造成影响,这种情况下对于内部节点只需要使用读锁就可以,也不需要对是内部节点的子节点进行安全判断,但是需要对是叶子节点的子节点进行安全判断,如果不安全,就要从根节点重新开始上写锁。
我们假设了大多数的操作是不需要 split 与 merge 的,因此这种乐观的实现方式可以带来更高的效率可以得到很大提升。